Как в Питоне создать матрицу?

В этой статье мы рассмотрим все концепции работы с матрицами в Python с нуля. Будет продуктивно, если вы напишите весь код самостоятельно по мере прочтения.

Прежде чем мы начнем, важно упомянуть, что Python не имеет встроенной поддержки матриц, подобных языкам, которые позволяют нам создавать многомерные массивы (C, C++, Java и т.д.). Python обеспечивает аналогичное поведение с использованием вложенных списков.

В этой части мы сосредоточимся на построении матриц со структурой данных на основе списка Python, чтобы получить базовое представление о построении матриц. А в последующих частях обсуждаются инструменты библиотеки Numpy.

Массивы

Рассмотрим последовательность из четырех чисел:

1 2 3 4

Давайте назовем эту последовательность A. Последовательность A обычно называется массивом, представленным в Python с помощью списка или кортежа. Этот массив A имеет длину 4. Мы обозначим его длину через n. Итак, для A n = 4. Приведенный ниже код показывает пример использования как списка, так и кортежа.

A = [1, 2, 3, 4] # список (list)

A = (1, 2, 3, 4) # кортеж (tuple)

В Python, если мы хотим получить доступ к отдельному элементу этого массива или сослаться на него, это делается с помощью числа, называемого индексом, для обозначения положения этого элемента в массиве. Индексы в Python начинаются с нуля. Для приведенного выше списка / кортежа индекс первого элемента равен 0, а последнего – 3. Приведенный ниже код выводит все элементы из списка с использованием индексов.

A = [1, 2, 3, 4]
print(A[0])
print(A[1])
print(A[2])
print(A[3])

'''результат''':
1
2
3
4

Поскольку списки могут содержать произвольное количество элементов, мы можем записать все операции со списками с помощью циклов. Ниже приведена обновленная версия предыдущего кода.

A = [1, 2, 3, 4]
'''цикл по элементам массива'''
for x in A:
    print(x)

'''или цикл по индексам массива'''
for i in range(len(A)):
    print(A[i]) '''обращаемся по индексу к элементу массива'''

'''результат''':
1
2
3
4
1
2
3
4

Матрицы

Матрица – это последовательность чисел, которая содержит два измерения. В отличие от массивов (также называемых векторами в математике), которые имеют одно измерение, то есть свою длину или размер, матрица имеет строки и столбцы. Матрица выглядит как прямоугольный блок чисел, содержащий m строк и n столбцов.

Пример матрицы:

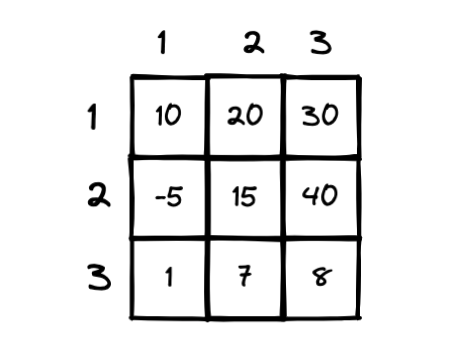
Назовем матрицу выше – М. Матрица M имеет 3 строки и 3 столбца. Первая строка, содержащая [10 20 30], и первый столбец, содержащий [10 -5 1]. M – это матрица размерностью 3 x 3 (3 на 3).

Доступ к элементам матрицы

Для доступа к одному элементу требуется указать индекс строки и индекс столбца. Итак, для ссылки на элемент в первой строке и первом столбце матрицы M мы напишем M₁₁ = 10

В общем случае формат – Mᵢⱼ, где i – номер строки, а j – номер столбца. В математике номера строк и столбцов начинаются с 1, а не с нуля (как в Питоне).

Вернемся к Python. Для хранения матрицы, нам нужно создать список состоящий из списков:

M = [
    [10, 20, 30],
    [-5, 15, 40],
    [1, 7, 8]
]

Для доступа к элементам нам теперь нужны два индекса: один для внешнего списка, а другой для внутреннего. Поскольку индексы начинаются с нуля, внешний индекс находится в диапазоне 0-2 (индекс строки), внутренний индекс также имеет диапазон 0-2 (индекс столбца).

Таким образом, к первому элементу (верхнему левому) можно получить доступ как к M[0][0], а к последнему – как к M[2][2].

M = [
    [10, 20, 30],
    [-5, 15, 40],
    [1, 7, 8]
]
print(M[0][0])
print(M[2][2])

''' напечатается:
10
8
'''

Чтобы вывести количество строк и столбцов, используйте функцию len().

Для строк получаем len() всей матрицы M, так как количество строк равно количеству списков во внешнем списке. Для столбцов нужно вызвать функцию len() для внутреннего списка.

M = [
    [10, 20, 30],
    [-5, 15, 40],
    [1, 7, 8]
]
print('Rows: ', len(M))
print('Columns: ', len(M[0]))
print('Matrix size: ', len(M), 'x', len(M[0]))

''' напечатается:
Rows:  3
Columns:  3
Matrix size:  3 x 3
'''

Чтобы получить доступ к одной целой строке, скажем, ко второй (т.е. к индексу 1), нужно сделать следующее:

M = [
    [10, 20, 30],
    [-5, 15, 40],
    [1, 7, 8]
]
print(M[1])

''' напечатается:
[-5, 15, 40]
'''

Печать столбцов не так проста, поскольку единственный способ доступа к данным – через индексы. Для печати элементов первого столбца единственным способом является следующий код:

M = [
    [10, 20, 30],
    [-5, 15, 40],
    [1, 7, 8]
]
for i in range(len(M)):
    print(M[i][0])

''' напечатается:
10
-5
1
'''

Приведенный ниже код печатает все элементы матрицы M:

M = [
    [10, 20, 30],
    [-5, 15, 40],
    [1, 7, 8]
]
for i in range( len(M) ): 
  ''' индексы строк от 0 до 2 '''
  for j in range( len(M[i]) ): 
    ''' индексы столбцов от 0 до 2 '''
    print( M[i][j] )

''' напечатается:
10
20
30
-5
15
40
1
7
8
'''

Приведенный выше код использует вложенные циклы for для печати всех элементов по строкам. Но результат не очень похож на матрицу. Для печати в матричном формате нам необходимо использовать некоторые возможности функции print:

M = [
    [10, 20, 30],
    [-5, 15, 40],
    [1, 7, 8]
]
for i in range( len(M) ):
  for j in range( len(M[i]) ):
        ''' вместо новой строки печатаем пробел '''
        print( M[i][j] , end = ' ') 
  ''' переход на новую строку после печати строки матрицы '''
  print() 

''' напечатается:
10 20 30 
-5 15 40 
1 7 8 
'''

Если вы не понимаете приведенные выше вложенные циклы, посмотрите измененный код ниже, который печатает индексы вместо данных. Это поможет понять, как работают с индексами в матрицах.

M = [
    [10, 20, 30],
    [-5, 15, 40],
    [1, 7, 8]
]
for i in range( len(M) ):
  for j in range( len(M[i]) ):
    ''' печать индексов: '''
    print( (i,j) , end = ' ') 
  print()

''' напечатается:
(0, 0) (0, 1) (0, 2) 
(1, 0) (1, 1) (1, 2) 
(2, 0) (2, 1) (2, 2) 
'''

Специальные виды матриц

Можно выделить следующие виды матриц, основываясь на их размерностях:

Квадратная матрица

Квадратная матрица – это матрица, имеющая одинаковое количество строк и столбцов.

Есть несколько свойств, связанных с квадратными матрицами, которые мы увидим в следующих разделах.

Вектор-строка

Вектор строка – это матрица, в которой количество строк равно единице, т.е. матрица размерностью 1 x n.

Пример:

Но представление с помощью списков Пайтон может быть немного сложным. Мы представим его в виде списка, содержащего один вложенный список:

row_vector = [ [10, 20, 30] ]

Вектор-столбец

Теперь очевидно, что матрица с одним столбцом, но с несколькими строками станет вектором-столбцом. т.е. размер будет m x 1

col = [[10],
      [20],
      [30]]

Это был краткий экскурс в мир матриц Питона.

В следующих статьях этого цикла мы рассмотрим более подробно работу с матрицами.